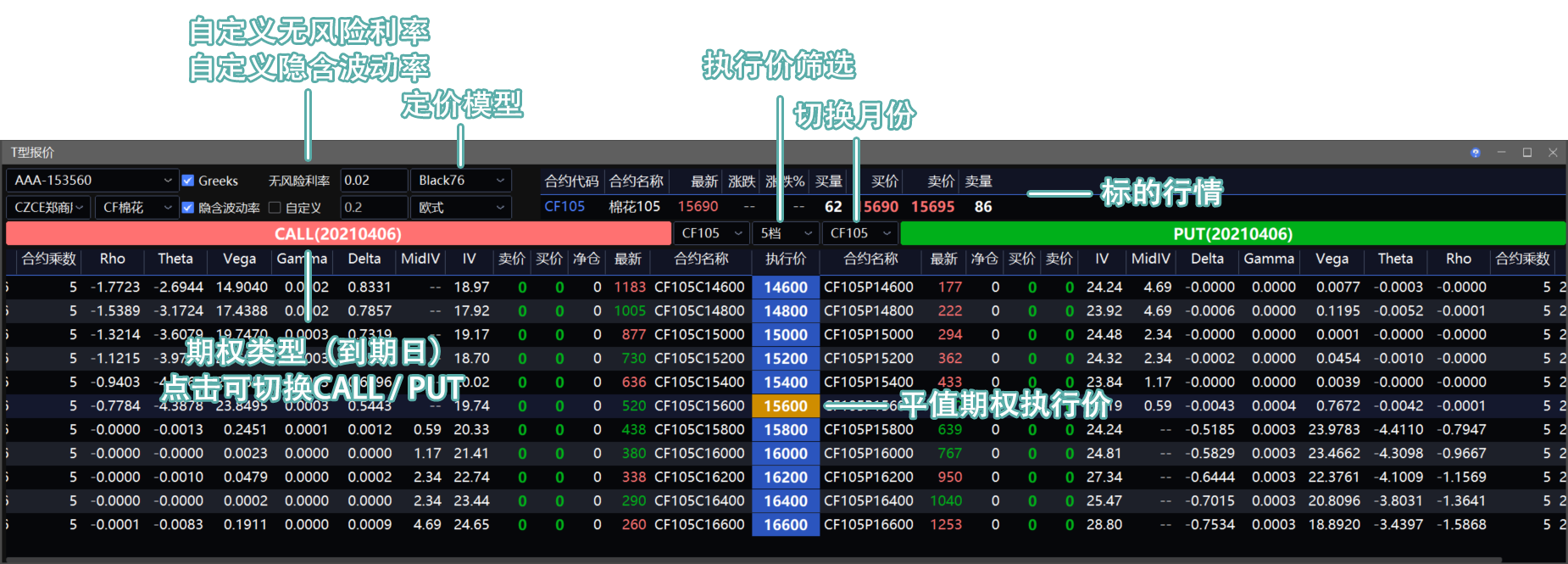
T型报价

期权的T型行情，包含基础行情、Greeks 指标、隐含波动率、期权对应的标的行情等。

位置：菜单 - 期权 - T型报价

视频：不止 T 型报价，万物皆可“T” by 王鼎

T型报价支持窗口多开、支持灵活切换 CALL / PUT 期权、切换不同月份。

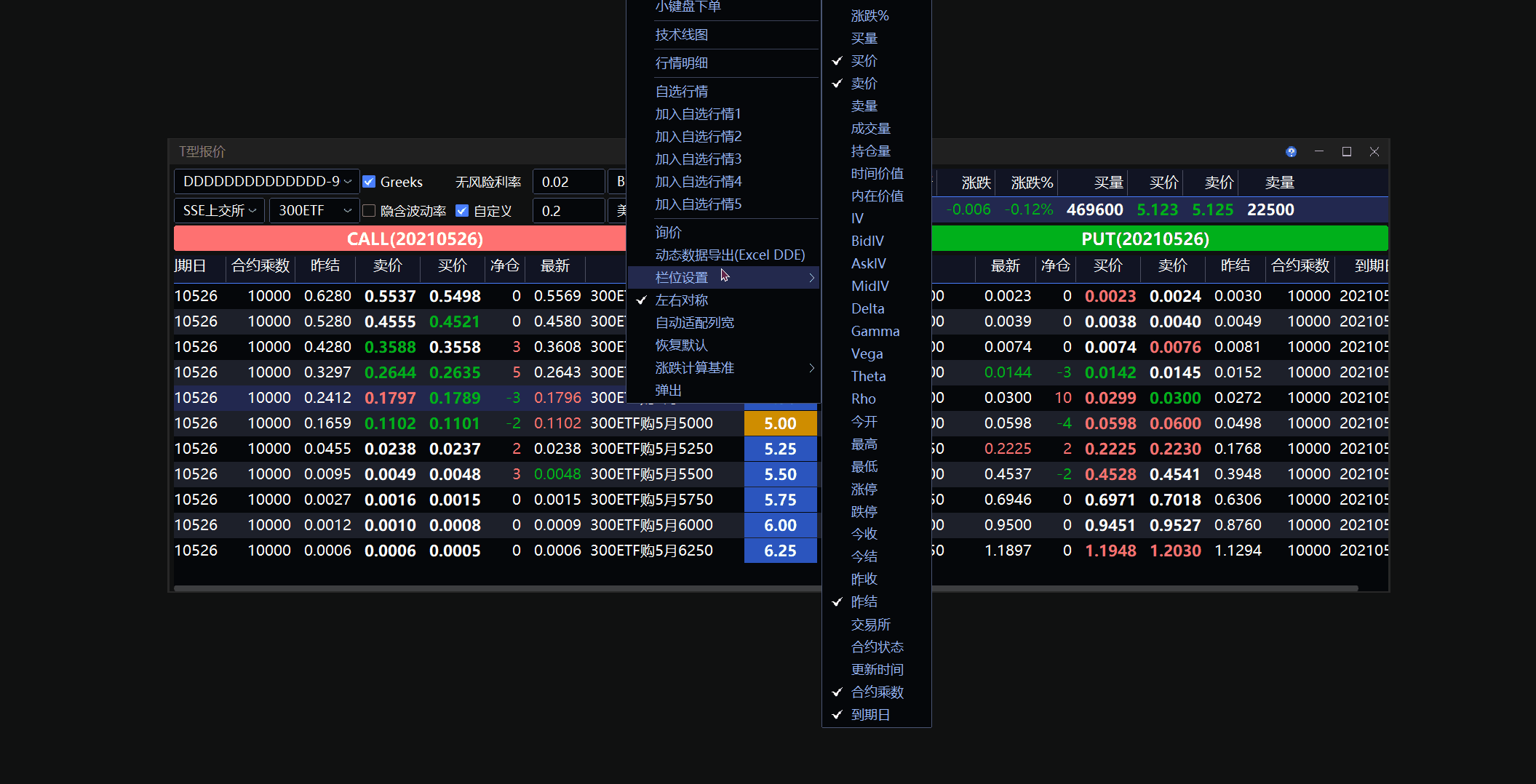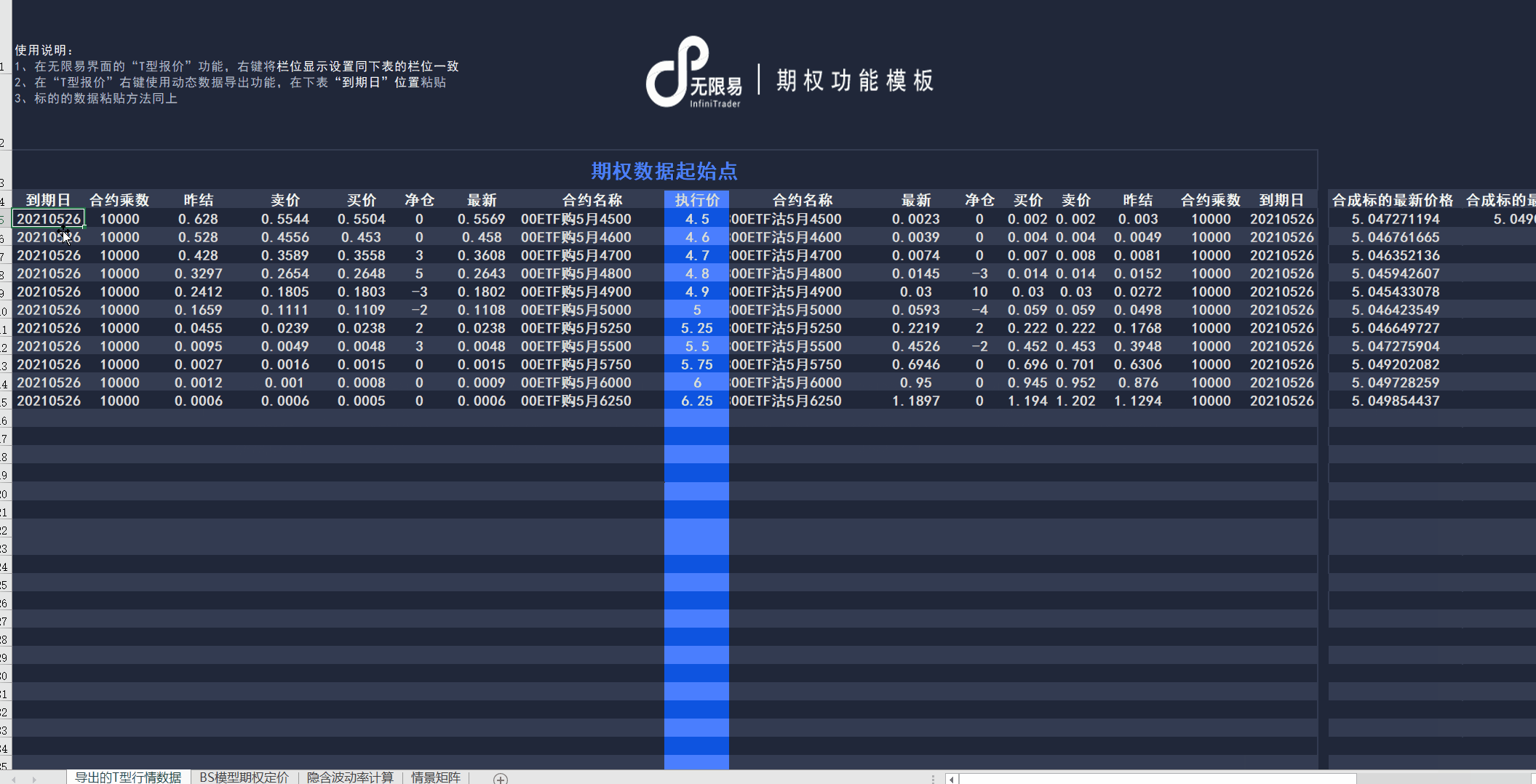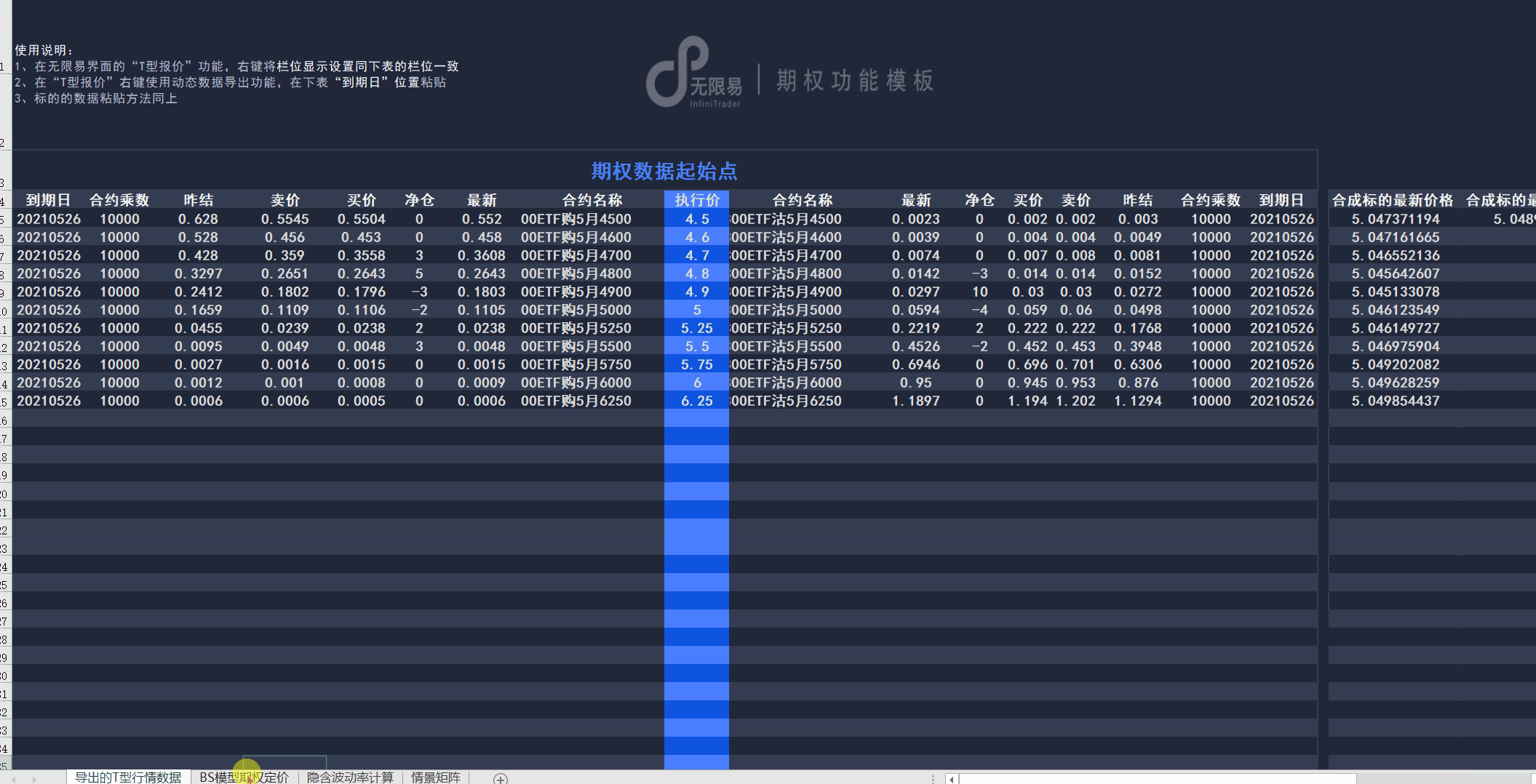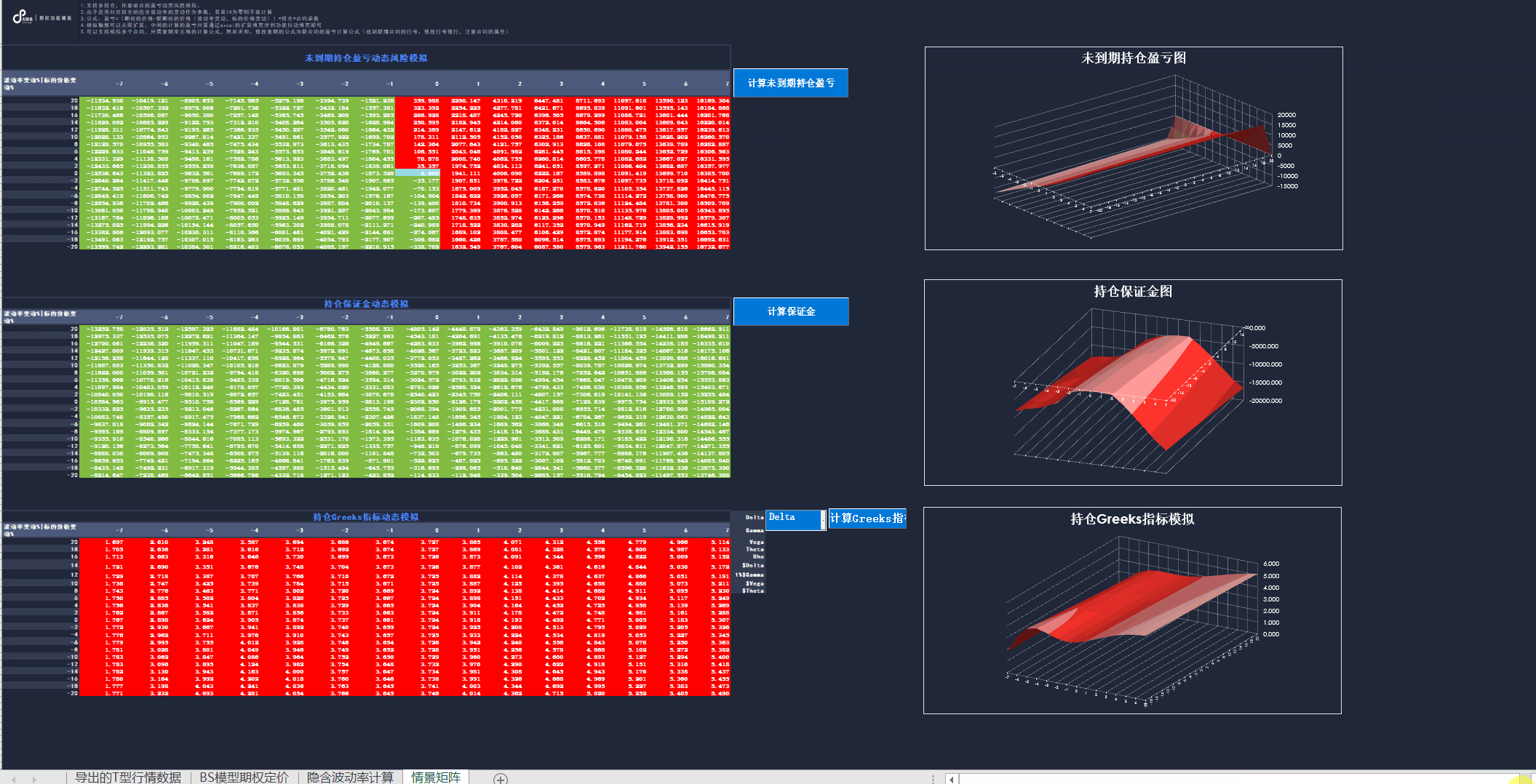
导出动态行情 DDE

可导出行情、持仓、盈亏等动态数据，利用 Excel 函数等功能统计分析，详见 Excel DDE 使用方法。

无限易内置5种算法

参数说明

后续计算公式的参数说明：

$S$ 标的价格

$K$ 执行价

$T$ 剩余到期天数，年化

$r$ 无风险利率

$\pi$ 交易组合价值

$\sigma$ 波动率

$Multiplier$ 合约乘数

$IV$

无限易计算的希腊值基于 T 型报价左上角选择的公式进行计算：

无限易内置 5 种模型方法，用于计算欧式期权和美式期权的隐含波动率。

其中需要用户自己设置:

1. 无风险利率

2. 欧式期权/美式期权

其中最常用的为 BS 公式：

$CallPrice = SN(d_1)-Ke^{-rt}N(d_2)$

$PutPrice = Ke^{-rt}N(-d_2)-S_0N(-d_1)$

$d_1=\frac{ln(S_0/K)+(r+\sigma^2/2)*T}{\sigma \sqrt T}$

$d_2 = d_1-\sigma \sqrt T$

将市场价格带入，反推出 $\sigma$ ，就是我们的隐含波动率。

注意：

1. 时间计算单位为年，一年总数无限中设置为 365，而不是 250
2. 计算时标的价格，无限易是使用标的价格的远期价格来计算。

$Delta$

期权价格变动与其标的资产价格变动的比率。

$Delta =\frac{\partial \pi}{\partial S}$

在不考虑股息率的情况下，使用 BS 公式推算出来的 Delta 公式为

$Delta_c = N(d_1)$

$Delta_p = N(d_1)-1$

$\$ Delta$

表示标的价格变动 1%，期权价格的变化量，公式如下：

$\$ Delta = S*Multiplier*Delta$

注意：

1. 如果是持仓，还需要乘以数量
2. 标的价格：合成期货价格

$Gamma$

交易组合中 Delta 的变化与标的资产价格变化的比率，是一个交易组合关于标的资产价格的二阶偏导数。当其比较小的时候 Delta 相对于标的资产价格变化比较慢，当其较大的时候，Delta 关于标的资产价格变化比较快。

$gamma = \frac{\partial \pi}{\partial S^2}$

注意： 这两个都是关于标的资产价格求导，而不是关于时间

在不考虑股息率的情况下，使用 BS 公式推导出来，公式应该为：

$gamma = \frac{N'(d_1)}{S *\sigma*\sqrt T}$

$\$ Gamma$

表示是标的价格变动 1%，cash delta 的变化量。也记作 1% cash gamma，公式如下：

$\$ Gamma = \frac{S^2}{100}*Multiplier*Gamma$

注意：

1. 如果是持仓的，需要乘以数量
2. 标的价格：合成期货价格

$Theta$

交易组合价值变化与时间变化之间的关系

$Theta = \frac{\partial\pi}{\partial t}$

在不考虑股息率的情况下，使用 BS 公式推导出来，公式应该为：

$Theta_c = -\frac{SN'(d_1)\sigma}{2\sqrt T}-rKe^{-rt}N(d_2)$

$Theta_p = -\frac{SN'(d_1)\sigma}{2\sqrt T}+rKe^{-rt}N(-d_2)$

其中：

$N'(d_1)=\frac{e^{-d_1^2/2}}{\sqrt {2\pi}}$

注意： 关于 Theta 值无限易除以了 365，计算的是每天的价值变化

$\$ Theta$

时间每变化 1 天，交易组合价值的变化，公式如下：

$\$ Thega = Multiplier*\frac{Theta}{365}$

注意：

1. 如果是持仓的，需要乘以数量
2. 无限易中的 Theta 已经除以了 365，不需要重复除了

$Vega$

交易组合价值变化与标的资产波动率变化的比率

$Vega = \frac{\partial \pi}{\partial \sigma}$

在不考虑股息率的情况下，使用 BS 公式推导出来，公式应该为：

$Vega = S\sqrt TN'(d_1)$

注意： 无限易是将计算出的 Vega 再除以了 100，即 1% 标的波动率变化对应的交易组合价值变化量

$\$ Vega$

标的资产波动率变动 1%，交易组合价值的变化，公式如下：

$\$ Vega = Multiplier*1 \% *Vega$

注意：

1. 如果是持仓的，需要乘以数量
2. 无限易的 Vega 已经乘以了 1%，所以不需要再乘以 1%

$Rho$

交易组合价值变化与利率变化的比率

$Rho = \frac{\partial \pi}{\partial r}$

在不考虑股息率的情况下，使用 BS 公式推导出来，公式应该为：

$Rho_c = KTe^{-rT}N(d_2)$

$Rho_p=-KTe^{-rT}N(-d_2)$

注意：

1. 无限易是将计算出的 Rho 再除以 100，即 1% 利率变化情况下，交易组合价值变化情况